СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ

Основные понятия и определения.

Сфера - геометрическое место точек в пространстве, равноудаленных от одной точки.

Шар – часть пространства, заключенного внутри сферы.

Радиус сферы – Отрезок прямой, соединяющий центр сферы с любой её точкой.

Ось - отрезок прямой, проходящий через центр сферы и соединяющий две её точки.

Окружность малого круга (Дуга Малого Круга) – окружность, полученная от сечения сферы плоскостью, не проходящая через центр сферы.

Дуга большого круга – Окружность полученная от сечения сферы плоскостью, проходящая через центр сферы.

Полюса окружности большого круга (P и P`)-точки на поверхности сферы, полученные от пересечения её осью, перпендикулярны окружности большого круга.

Сферический радиус – дуга большого круга, от полюса, до любой точки на поверхности сферы.

Экватор – окружность большого круга, полученная от сечения сферы плоскостью проходящей через её центр и перпендикулярный её оси.

Меридиан – дуги больших кругов, проходящих через полюса.

Сферический перпендикуляр – дуга большого круга, перпендикулярная другой ДБК.

Дуги больших кругов, подобно прямым на плоскости обладают следующими свойствами:

1. Через 2 любые точки на сфере, не лежащие на одной оси можно провести только одну ДБК.
2. ДБК меньшая 180 градусов является кратчайшим расстоянием между двумя точками на сфере.
3. Положение любой точки на сфере может быть определено в прямоугольной системе координат (по X, Y,Z)
4. Или в полярной системе координат, с началом в центре сфере и направляющими углами Фи и Лямбда.

СФЕРИЧЕСКИЙ ТРЕУГОЛЬНИК

СВОЙСТВА СФЕРИЧЕСКИХ ТРЕУГОЛЬНИКОВ

Сферической тригонометрией рассматриваются фигуры только смощью ДБК.

Длина ДБК пропорциональна центральному углу.

По определению Эйлера сферической тригонометрией на сфере рассматриваются фигуры, образованные с помощью ДБК меньшей, либо равной 180градусов.

Двуугольник – простейшая фигура на сфере (EPP`G), образованная двумя ДБК.

LEOG=LEPG=LEP`G=GE

Мерой сферического угла является двугранный угол – EPP`G

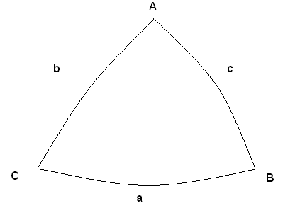
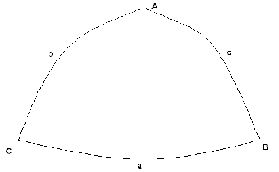
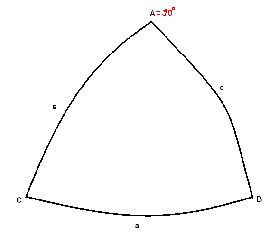
Сферический треугольник – фигура на сфере, образованная пересечением трех ДБК меньшими 180 градусов.

Вершины сферического треугольника – точки пересечения ДБК.

Треугольник АВС – сферический треугольник

АВС - вершины

При пересечении трёх ДБК образуется четыре пары зеркальных треугольников.

Учитывая, что стороны и углы этих треугольников являются взаимным дополнением до 180 градусов то достаточно рассмотреть один треугольник АВС.

Мерами углов сферического треугольника являются двугранные углы трехгранного угла ОАВС.

Мерами сторон сферического треугольника являются плоские углы трехгранного угла.

Коперник предложил образовывать сферический треугольник пересечением трехгранного угла со сферой, причем вершина трехгранного угла совпадает с центром сферы. Отсюда все свойства трехгранного угла можно перенести на свойства сферического треугольника.

Если измерить два сферических треугольника в угловой мере то треугольники равны.

Учитывая это формулы и выводы сферической тригонометрии, полученные для сферы одного радиуса полностью справедливы для сферы другого радиуса. И для упрощения расчетов принимаем радиус, равный единице.

Все сферические треугольники, зависимости от значений элементов можно разделить на:

1. Косоугольные - элементы, равные 90 градусов отсутствуют.
2. Прямоугольные – имеют хотя бы 1 угол, равный 90 градусов.
3. Четвертной – Имеют хотя бы одну сторону, равную 90 градусов.

На основании свойств трехгранного угла получаем свойства сферического треугольника:

1. Сумма сторон сферического треугольника больше нуля но меньше 360 градусов.
2. Любая сторона сферического треугольника меньше суммы но больше разности двух других сторон.
3. Сумма трех углов больше 180е но меньше 540 градусов.

Сферический избыток – превышение суммы углов сферического треугольника над 180 градусами. E=A+B+C-180

По сферическому избытку можно судить о треугольнике в целом и найти его площадь.

S_ABC = II*R²/180*E

4)Сумма двух углов сферического треугольника без третьего менее 180 градусов.

5) Если сумма двух углов сферического треугольника больше, равна или меньше 180 градусов то и сумма противолежащих им сторон соответственно равна больше, меньше, или равна 180 градусам.

6) если разность двух любых углов сферического треугольника больше, меньше или равна нулю то разность двух противолежащих сторон больше, меньше или равна нулю соответственно.

Если одно из вышеперечисленных свойств не соблюдается, то сферический треугольник не существует.

ВЗАИМНОПОЛЯРНЫЕ СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ

Два треугольника, лежащие на одной и той же сфере, называются взаимно полярными, если вершины одного из них является стороной другого.

Теоремы о взаимно полярных сферических треугольниках:

1. Сумма угла исходного сферического треугольника и противолежащей стороны полярного ему треугольника равна 180 градусов.
2. Сумма угла полярного сферического треугольника и противолежащей стороны исходного треугольника равна 180градусов: А`+a = 180градусов

B`+b=180; C`+c=180;

Для доказательства данных теорем продолжим стороны исходного сферического треугольника до пересечения его с полярным.

В=MN

b`=A`M+MN+MC`

B`=KL=KA+AC+CL

b=AC

B+b`=MN+A`M+MN+NC`=180

B`b=KA+AC+CL+AC=180

MN+A`N=90градусов-сферический радиус стороны «а» треугольника АВС с полюсом в вершине «а`»

MN+NC`=90градусов- Сферический

КА+АС=90 сферический радиус стороны С` треугольника

CL+AC=90 сферический радиус стороны А` треугольника A`B`C` с полюсом в вершине А

По условию построения взаимно полярных треугольников сферический радиус был взят равным 90градусов, следовательно (3.1) (3.2) доказывают теоремы о взаимно полярных треугольниках.

СИСТЕМЫ ИЗМЕРЕНИЯ СТОРОН И УГЛОВ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА.

Для измерения углов и сторон сферического треугольника используются одни и те же системы и единицы измерения:

1. Радианная

2. Градусная

3. Временная

4. Десятичная

Радианная система - измерения дуг и углов является удобной при описании вращательных действий при аналитических формул и теоретических выкладках. Радианной мерой обобщенной дуги (центрального угла, опирающегося на эту дугу) называется отношение длины этой дуги к длине её радиуса. Где а-центральный угол L-длина дуги и R-длина дуги, единицей измерения в данной системе является радиан. a=L/R;

Радиан-центральный угол, опирающийся на дугу, длина которой равна одному радиусу.

Так как отношение длины окружности к длине радиуса равно 2П то окружность содержит 2П радиана или 6,23 радиусов сферы.

Градусная система — система измерения дуг и углов, одна из самых древних систем. Градус- есть центральный угол, соответствующий дуге 1/360 части окружности.

Градус делится на 60 минут минута на 60 секунд. Таким образом в полной окружности:

360градусов=2600минут=189600секунд

Градусная и радианная системы связаны следующим соотношением:

а^рад/a˚=2П/360˚

Для применения данного выражения используют следующие дуги:

1˚1`1``= рад

arc1˚ = 2П/360˚= 1/57,3˚

arc1` = 2П/360˚*60 = 1/3438

arc 1`` = 2П/360˚*60*60 = 1/206265

ОСНОВНЫЕ ФОРМУЛЫ СФЕРИЧЕСКОЙ ТРИГОНОМЕТРИИ

Основными формулами называются формулы, связывающие три заданных треугольника с одним искомым количество основных формул.

Для решения сферического треугольника нужно 15 формул.

Для вывода основных формул используются:

Элементы теории проекций, аналитические и графические методы, векторная алгебра, географические координаты и.т.д.

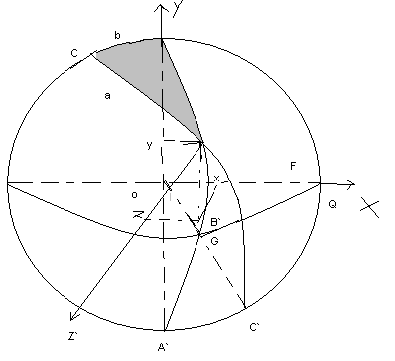
Угол АОВ = С

Угол ВОС = 90˚- С

Угол GOQ = 180˚ - A

Угол GOZ = A – 90˚

OB` = R cos (90˚ - C) = R sin c

x= OB` * cos (180˚- A) = R sine cosA

y = R * cos c

z = OB` cos1A – 90˚ = R * sin c * sin A

по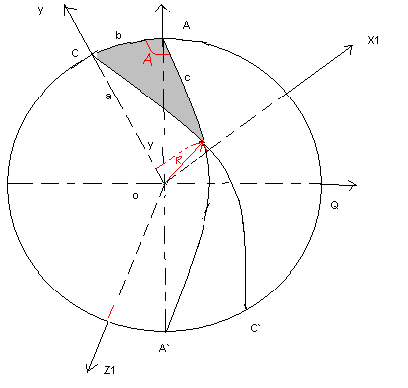вернем прямоугольную систему координат OXYZ вокруг оси OZ на угол равный дуге AC (стороне b) в положение OX1Y1Z1 чтобы ось OY1 проходила через вершину С сферического треугольника АВС.

Найдем прямоугольные координаты x1 y1 z1 вершины В в новой системе координат.

Ц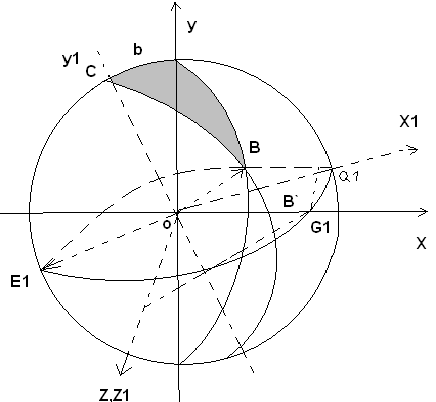ентральные углы радиус вектора ОВ с осями OX1, OY1, OZ1, новой системы координат равны:

Проекция вектора ОВ на OY1, OZ1, в новой стеме координат определяется выражением: OB1=R * cos(90-a)=R sin a

Прямоугольные вершины сферического треугольника АВС в новой системе координат определяются выражением

Системы уравнений связывают прямоугольные координаты точки В на сфере со сферическими координатами. В настоящее время используются в спутниковой навигации.

Из геометрии тригонометрии известно, что при поворте осей координат (на угол равный стороне b) координаты одной и тойже точки в разных системах корординат связаны с собой соотношением:

X₁ = X cos b + y*sin b

Y₁ = - sin b + y cos b

Z₁ = Z

(5.3)

подставим выражение 5.1 и 5.2

R*sin a cos C = R*sin c * cosA*cos b +R*cos c * sin b

R*cos a = R*sin c cosA*sin b + R*cos c * cos b

R*sin a * sinC = R*sin c * sinA

sin a cos C = sin c * cosA*cos b +cos c * sin b

cos a = sin c cosA*sin b + cos c * cos b

sin a * sinC = sin c * sinA

(5.4)

Система (5.4) представляет собой вю сферическую тригонометрию.

ФОРМУЛА (ТЕОРЕМА) СИНУСОВ.

Представляет собой третью теорему системы 5.4 и имеет следующую формулировку:

Произведение синуса стороны на синус ближайшего угла равен произведению синусов противолежащих им элементов сферического треугольника.

Sin a/Sin A = Sin b/Sin B=Sin c/Sin C

Практическое решение при этой формуле имеет недостаток, невозможно определить по знаком тригонометрической функции синусов четверть искомого элемента, так как элементы сферического треугольника имеют значения в пределах 0-180 (1ая 2ая четверти) а синусы углов в обеих четвертях имеют положительный знак.

ТЕОРЕМА КОСИНУСОВ СТОРОНЫ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА

Представляет выражение второе системы 5.4 и объединяет 3 стороны и 1 угол.

В сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих двух сторон на косинус угла между ними.

Cos a = Cos b*Cos c + Sin b*Sin a*Cos A

Cos b = Cos a*Cos c + Sin a*Sin c*Cos B

Cos c = Cos a*Cos b + Sin a*Sin b*Cos C

Практическое применение в вычеслении высот небесных светил (астрономия), расстояние между двумя точками, плавание по ДБК.

ТЕОРЕМА КОСИНУСА УГЛА СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА

Может быть получена из формулы косинуса стороны, используя свойство взаимнополярных треугольников.

Cos a = Cos b*Cos c + Sin b*Sin c* Cos A

a=180-A b=180-B c=180-C A=180-a

Cos A = - Cos B*Cos C + Sin B*Sin C*Cos a

Cos B = - Cos A*Cos C + Sin A*SinC*Cos b

Cos C = - Cos B*Cos A + Sin B*Sin A*Cos c

В сферическом треугольнике косинус угла равен отрицательному произведению двух других углов, плюс произведение синусов этих углов на косинус стороны между ними.

ФОРМУЛА ПЯТИ ЭЛЕМЕНТОВ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА

В сферическом треугольнике произведение синуса стороны на косинус прилегающего угла, равно произведению косинуса стороны, противолежащей этому углу на синус третьей стороны, минус произведение синуса противолежащей стороны на косинус третьей стороны, и на косинус угла между этими сторонами.

Sin a*Cos C = Cos c*Sin b – Sin c*Cos b*Cos A

Sin a*Cos B = Cos b*sin c – Sin b*Cos c*Cos A

Sin C*Cos В = Cos b*Sin a – Sin b*Cos a*CosC

Sin C*Cos A = Cos a*Sin b – Sin a*Cos b*CosC

Sin b*Cos A = Cos a*Sin c – Sin a*Cos c*CosB

Sin b*Cos C = Cos c*Sin a – Sin c*Cos a*CosB

Формулы объединяют пять элементов — 3 стороны и 2 угла.

Sin B*Cos c = Cos C*Sin A – Sin C*Cos A*Cos b

Sin B*Cos c = Cos A*Sin C – Sin A*Cos C*Cos b

Sin A*Cos b = Cos B*Sin C - Sin B*Cos C*Cos a

Произведение синуса угла на косинус прилежащей стороны равно произведению косинуса угла противолежащего этой стороне на синус третьего угла минус произведение синусов противолежащего угла на косинус третьего угла и на косинус стороны между этими углами.

Практическое применение: Теоритический вывод.

ФОРМУЛА КОТАНГЕНСОВ (ФОРМУЛА ЧЕТЫРЕХ РЯДОМ РАСПОЛОЖЕННЫХ ЭЛЕМЕНТОВ)

Получаем из выражения 9.1 Делением их на выражение теоремы синусов.

Sin c/Sin C = Sin a/ Sin del

Sin c = Sin a*Sin C/Sin A

Sin a*Cos C/Sin a*Sin C*Sin A = Cos c/Sin c*Sin b = Sin c/Sin c*Cos A

Ctg C*Sin A = Ctg c*Sin b – Cos b*Cos A

В сферическом треугольнике произведение котангенса крайнего угла на синус среднего равно произведению котангенса крайней стороны на синус средней стороны, минус произведение косинусов средних элементов.

РЕШЕНИЕ ПРЯМОУГОЛЬНЫХ И ЧЕТВЕРТНЫХ СФЕРИЧЕСКИХ ТРЕУГОЛЬНИКОВ

Прямоугольным называется сферический треугольник, у которого хотябы один угол равен 90 градусов, а четвертным, у которого хотя бы одна из сторон равна 90 градусов, т. е. Четверти, окружности большого круга. Прямоугольный треугольник можно решать по основным формулам сферической тригонометрии, но учитывая, что тригонометрические функции и элементы могут быть равны 90 градусов и равны 1 или 0, поэтому и формулы сферической тригонометрии могут быть значительно упрощены. Первыми заметили и предложили своё правило решения подобных треугольников (прямоугольные и четвертные) ученые Модюи и Непер.

Правило Модюи-Непера:

Если элементы прямоугольного или четвертного сферического треугольника расположить в круге Непера, исключая элемент, равный 90 градусов и заменяя смежным(прилегающщим к нему) элементом дополнения до 90 градусов, а угол противолежащей стороне 90 градусов дополнением до 180градусов, то косинус любого элемента равен произведению котангенсов смежных (прилежащих элементов) или произведению синусов не смежных (дальних элементов).

Прямоугольный треугольник

Sin b = Ctg C*Tg c; Sin b = Sin a*Sin b

Sin c = Ctg B*Tg b; Sin c = Sin a*Sin C

Coc B = Ctg a*Tg c; Cos B = Sin C*Cos b

Cos C = Ctg a*Tg b; Cos C = Sin B*Cos c

Четвертной треугольник

Cos A = - Ctg b*Ctg B; Cos A = - Cos B*Cos C

Sin B = CtgCtg C; Sin B = - Sin A*Sin b

…...................................................

Свойства:

1)В прямоугольных и четвертных сферических треугольниках противолежащие элементы всегда раполагаются в одной и тойже четверти. В первой или второй.

ДОПОЛНИТЕЛЬНЫЕ ФОРМУЛЫ СФЕРИЧЕСКОЙ ТРИГОНОМЕТРИИ

Кроме основных формул имеются и дополнительные формулы:Формулы полупериметра, сферического избытка, Деланбера-Гаусса, Аналогии Непера.

Использование дополнительных формул позволяет повысить точность вычислений или уменьшить их объём.

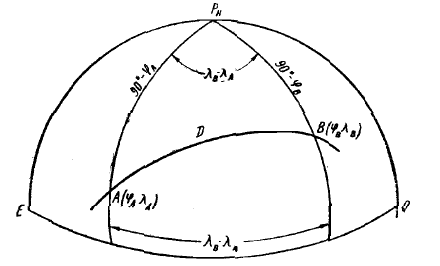
СФЕРИЧЕСКОЕ СХОЖДЕНИЕ МЕРИДИАНОВ

Это разность направлений в ортодромии в начальной и конечной точках Gam=A₂-A₁

Для определения значений угла схождения меридианов и их зависимости от координат точеквоспользуемся аналогиями Неппера для сферического навигационного треугольника.

Tg*((180-A2)+A1)/2=Cos(((90-Фи1)-(90-Фи2))/2)Cos(((90-Фи1)+(90-Фи2))/2)* Ctg (del*Lam)/2

Tg Gam/2=(SinФи_ср/Cos (del*Фи/2))*Tg (del* Lam)/2

Фи_ср=(Фи₁+Фи₂)/2

В навигации используется понятие ортодромичекой поправки. Ортодромическая поправка это разность между направлениями от одного пункта в другой по ортодромии или локсодромии.

Кси=ЛокА-А_орт

Кси=Gam/2=((del*Lam)/2)*sin_ср

В МТ приведены ортодромические поправки как разность геодезической линии и локсодромии.

РАСЧЕТ ПЛАВАНИЯ ПО ОРТОДРОМИИ (ДБК)

Общие принципы расчета плавания:

1. Оценка целесообразности плавания судном по ДБК, оценка целесообразности осуществляется спомощью таблицы 23Б, МТ-75 или выражением:

del*S%=100%(S_орт-S_локс)/S_орт

del*S%=Кси²/200

Где S% Относительная разность расстояний между портами отхода и прихода для оперативной оценки можно использовать:

del*S= S_орт-S_локс

Где Кси=Gam/2=(Kk-Kн)/2

2. Задание ДБК:

а) По координатам двух точек.(Фи_нLam_н ),(Фи_кLam_к)

б) По координатам любой точки и направлению в этой точке (Фи_iLam_i К_i )

б1) По точке пересечения ДБК с экватором и курсом в этой точки

б2) По координатам точки вертекса(точка ДБК с наибольшей широтой)задается (Фи_верт Lam_вер) Курс=90(270) ДБК меридиан пересекает под углом 90 градусов а все другие под разными углами.

2. Построение ДБК спомощью ортодромичечской поправки и локсодромического треугольника.

3. Определяем промежуточные точки ДБК (Фи_iLam_i )

4. Замена ДБК отрезками локсодромий по промежуточным точкам (делается из расчета допустимых погрешностей длин локсодромий ортодромий или их направлениями)

РАСЧЕТ ПЛАВАНИЯ ПО ДБК

ПО ОСНОВНЫМ ФОРМУЛАМ

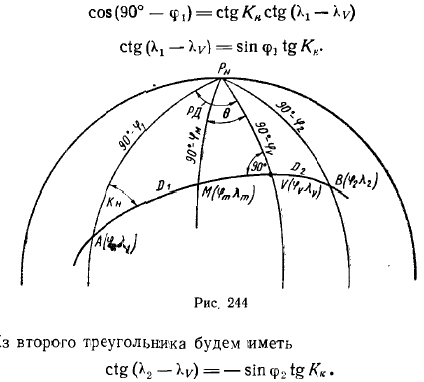
По заданным координатам (Фи₁Lam₁)(Фи₂Lam₂) получаем сферический треугольник АP_n В решение произволится по уравнениям ортодромии (см. параграф «уравнения ортодромии»)

S_орт

A₁=К_н

A₂=К _к

Воспользуемся уравнением или решением сферического треугольника АP_n V_i

Зная del*Lam, задаваясь долготой Lam_{i и} зная Курс начальный и I начальное получим выражение

Tg*Фи_i=CtgA₁*Sindel*Lam SecФи_н+TgФи_н

и спомощью него координаты промежуточных точек Фи_i Lam _i как правило выбирается кратным меридианам которые приведены на карте через промежуточные меридианы обеспечивающей заданные разницы(разница, точность) между длинами ортодромии и локсодромии. Для определения промежуточных курсов решается локсодромический треугольник, образованный локсодромией меридианами и параллелями промежуточных точек ДБК.

На карте равноугольно цилиндрической проекции (НМК) локсодромический треугольник прямоугольный, но необходимо помнить что его катеты имют различную рамерность (морские или экваториальные мили), что в свою очередь н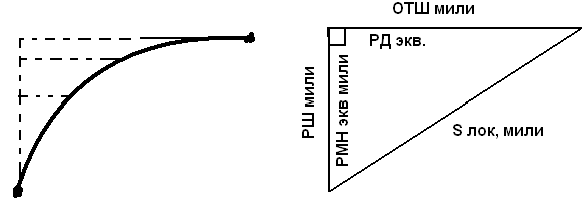еобходимо учесть при выводе следующих формул:

TgЛок.K=ОТШ/HL

TgЛок.К=РД/РМ2

Мч-меридиональная часть для Фиi из таблицы 26 МТ-75(Экваториальные мили)

Sлок-расстояние между соседними локсодромическими точками.

РД,РМч-разность долгот и меридиональная часть между сосдними лосодромическими точками(экв. мили)

ОТШ и РШ-отшествие и разность широт между соседними точками(мили)

Мч-рассотяние по меридиану от экватора до параллели в нормальной равноугольной цилиндрической проэкции.

ЗАДАНИЕ ДБК ОСНОВНЫМИ ФОРМУЛАМИ

Сводится к решению сферического треугольника по заданным координатам.

Задание ортодромии спомощью параметров ее пересечения с экватором.

Параметры пересечения ДБК с экватором K₀ и Lam₀ определеются независимым методом расчета из координа пунктов отхода и прихода на основе совмесного решения прямоугольных треугольников. Из пересечения W_оAW_н

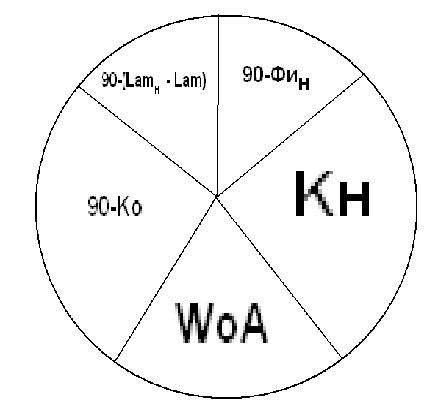
Параметры Lam0 и К0 можно найти независимо от начального курса и совместным решением 2-х треугольников.

Tg(Lam_н-Lam₀)=SinФи_н*TgК_н

TgK₀=Sin(Lam_н-Lam₀)*CtgФи_н

Cos(90(Lam_н-Lam₀))=Ctg(90-K₀)Ctg(90-Фи_н)

Cos(90(Lam_к-Lam₀))=Ctg(90-K₀)Ctg(90-Фи_к)

Освободимся от дополнения до 90 градусов, найдем разности, суммы и отношения, после преобразований получим выражение:

Tg(((Lam_к+Lam_н)/2)-Lam₀)=Tg(((Lam_к-Lam_н)/2)*Sin(Фи_к-Фи_н)

Lam ₀₂=Lam_о +или-180

Плавание по ортодромии определяется из решения этих же прямоугольных треугольников, как алгебраическая разница дуг.

Sорт=WoB-WoA

TgWoA=Tg(Lamн-Lamo)Cosec Ko

TgWoB=Tg(Lamк-Lamo)Cosec Ko

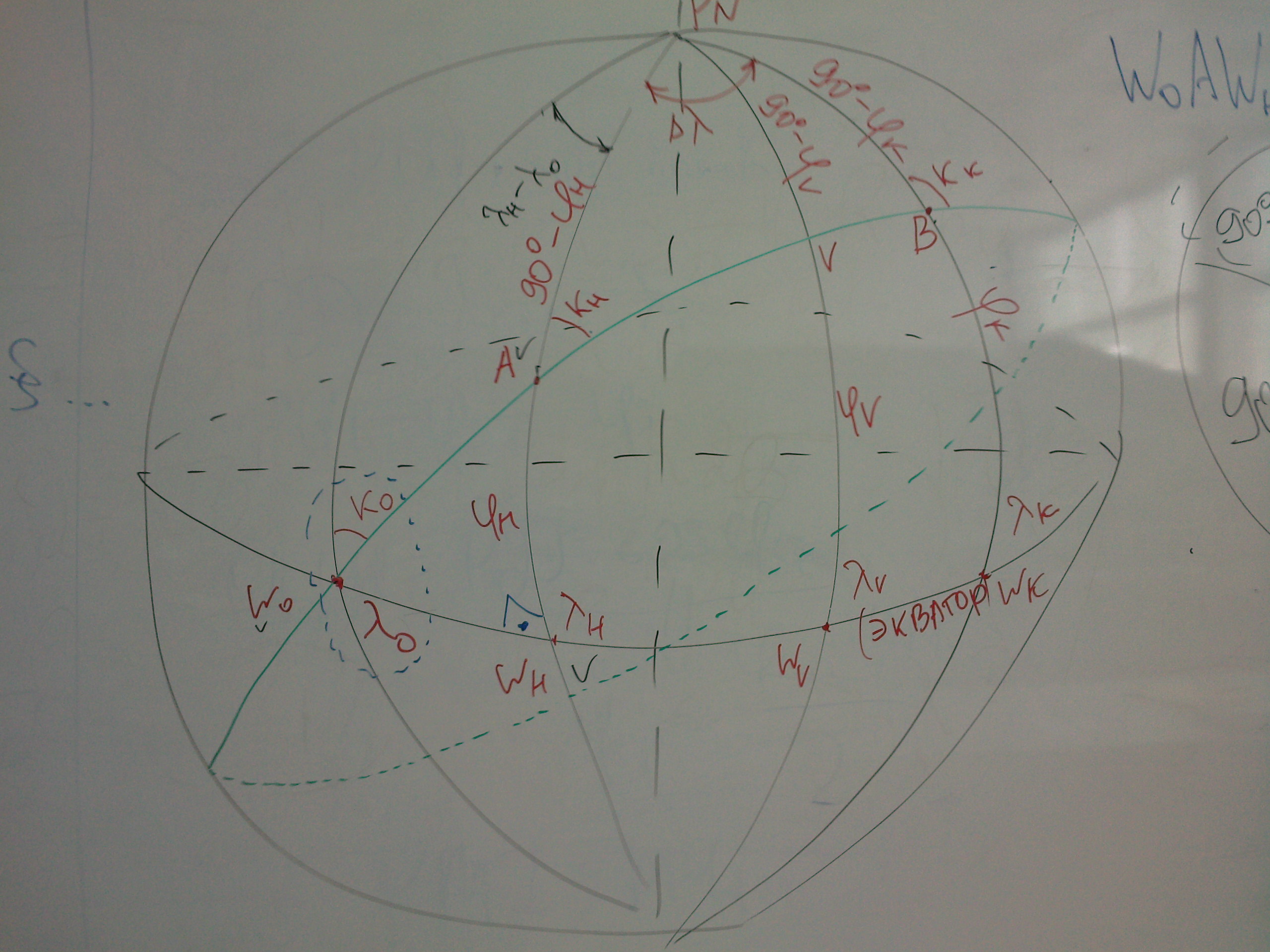
Расчет параметров ортодромии от вертекса:

Расчеты от вертекса базируютса на симметрии ортодромии относительно этой точки.

Кроме того ортодромия пересекает меридиан в точке вертекса под углом 90 градусов.

SinKo/Sin(90-Фи_v)=Sin90/Sin90=1

SinKo=Sin(90-Фи_v)

Ko=90-Фи_v

Cos(90-(Lam_о-Lam_v))=Ctg(90-Фи_v)Ctg(90-K_о)

Sin(Lam_о-Lam_v)=TgФи_v*TgKo и Sin(Lam_о-Lam_v)=1

Lam_v =Lam_о + или — 90

Ctg((Lam_{н —} Lam_н)/2) Sin(Фи_к-Фи_н)Cosec(Фи_к-Фи_н)

Для расчета ДБК через вертекс в судовождении используются специальные номограммы. Этот метод в основном используется на судах по иностранным флагом.

Промежуточные точки ДБК определяются из решения четвертных сферических треугольников.

TgФи_i = TgФи_v *Cos(Lam_i-Lam_v)

Где Lam_i – Доллгота промежуточных точек ДБК.

Через главные радиусы кривизны по формуле Эйлера можно получить радиус кривизны любого нормального сечения:

1/Ra=(Cos ² *А/M)+(Sin ² *A/N)

Ra - радиус кривины любого нормального сечения

А - азимут этого нормального сечения.

Через delA от 0 до 2П по вышеуказанной фрмуле находим радиусы а затем усредняем для получения среднего радиуса кривизны поверхности земного элипсоида. Выражение среднего радиуса сводится ко второй теореме Грунерта.

Rср= корень квадратный из MN

Средняя арифметическая радиусов кривизны равно среднегеометрическому главных радиусов кривизны. Геометрически это означает замены поверхности элипсоида сферой сферой с радиусом Rср в районе данной точки всего элипсоида. При этом должны соблюдаться условия:

1. Vсф=Vэл

2. Sпоб сф.=Sпов эл.

3. Равенство любых других дуг

4. Равенство длин меридианов

Из всего вышесказанного можно сделать вывод, главные радиусы кривизны изменяются с широтой, увеличиваясь от экватора к полюсу.

Фи=0

M=a(1-e²)

N = a

N>M

Фи=90

M=a/(1- e²) ^1/2

N=M

Главный радиус кривизны используется в судовождении при построении карт для определения длин дуг меридианов (параллелей)

В геометрическом смысле теорему о среднем радиусе кривизны земного элипсоида можно истолковать как замену элипсоида сферой со средним радиусом выделив несколько вариантов замены:

1. Радиус сферы равного объема селиксоида

2. Радиус сферы поверхность которой будет будет равновелика поверхности элипсоида.

3)Радиус сферы обеспечивает минимум разности расстояний между точками на сфере и элипсоиде.

4. Радиус сферы принимается равным значению R = 6366707м при котором соблюдается равенство — 1`ДБК=1м. миля=1852м

ДЛИНА ДУГ МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ.

МОРСКАЯ МИЛЯ

Необходимы при построении карт и расчетов плавания судна.

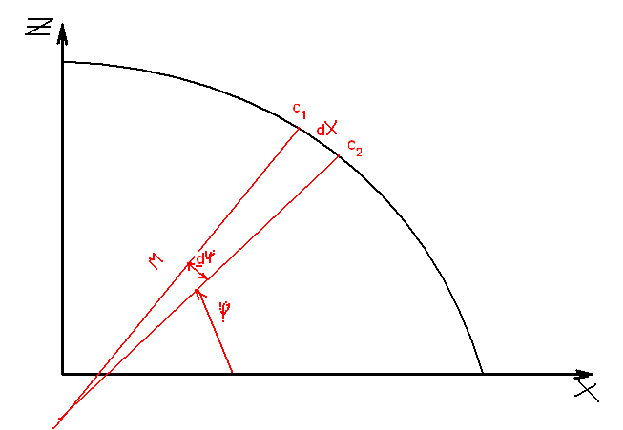
dx=M*dФи=(dФи*а(1-е²))/(1-e² Sin² Фи)^3/2

Для получения конечной дуги меридиана вышеуказанное выражение нужно проинтергировать в интервале широт Фи1 и Фи2 знаменатель выражения раскладывается вряд по Беному в Ньютонах. При это мсохраняется различне количество слагаемых от которых зависит точность приближения. После преобразований и подстановки длины дуги меридиана получим конечное выражение линейной длины одной минуты дуги меридиана которая и называется морской милей. Для элипсоида ПЗ-90 Длина дуги равна 1852,215-9,328*Cos2Фи.

Длина морской мили изменяется с широтой.

В 1928г. МГБ приняло стандартом морскую милю, равную 1852м.

Россия приняла в 1931г.

На ПЗ-90:

del=1852м — на широте 45 градусов.

Максимальная погрешность прокладки расстояния с использованием стандартной морской мили не будет превышать 0,5 градусов в районе полюсов и экватора. Формально это различие учитывается на морской карте.

Линейную длину дуги параллели можно определить через радиус кривизны первого вертикала (см. рисунок ниже)

В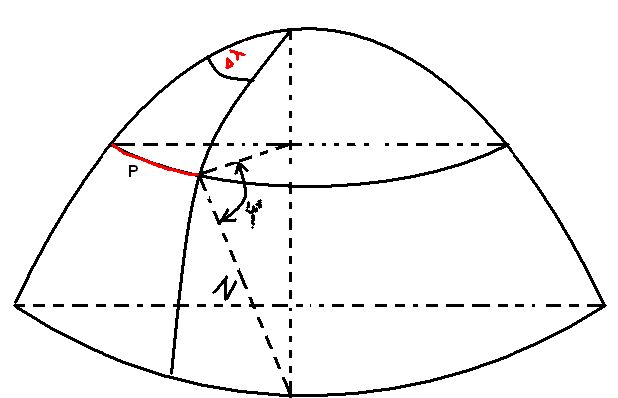 картографии имеет важное значение длина одной минуты дуги параллели (Экваториальная миля)

P₁ =a*CosФи.(1-е² Sin²Фи)^1/2

ПЗ-90(а,е), и Фи=0(Экв)

Pо =1855,324м= 1экв миля

Она постоянна для каждого элипсоида и снимается с верхней или нижней части карт.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ТОЧКИ НА ЗЕМНОЙ ПОВЕРХНОСТИ
ЗАДАННОЙ КООРДИНАТНОЙ СИСТЕМЕ

Основные координатные системы преведены в таблицах МТ 2000 (2.23-2.26) Известно что прямоугольные и географические координаты точки на поверхности Земли будут зависет от параметров референц элипсоида и места его привязки к поверхности земли, поэтому при использовании информации о координатах с различных геодезических систем (приборов или карт), координаты для дальнейшего использования необходимо приводить к координатной системе используемой карты. Иначе могут возникнуть погрешности до 1 мили. Имеются специальные требования IHO рез. S-60 по переводу систем координат. В настоящее время используется теория Молодетского для преобразования систем координат. Суть теории сводится к определению расхождения центров референции элипсоидов. Расчеты по переходу к системы VGS-84 преведены в таблице МТ 2000 2.24.

Для практических целей поправки географических координат для прехода к системе VGS-84 преведены на картах масштабов крупнее 1:500000(требования IMO и IHO). Для перхода от прямоугольных координат к географическим в приема-индикаторах GPS используются следуюие соотношения:

X=[N+H]CosФиCosLam

Y=[N+H]CosФиSinLam

Z=[N(1-e²)+H]*SinФи

N-радиус референц элипсоида

е — эрекстринцитет

H, Фи, Lam – Высота Широта и Долгота наблюдателя.

ООТШЕСТВИЕ

(ОТШ)

Из локсодромического треугольника на сфере следует:

ОТШ = dS* SinK = d*Lam N *CosФи

Интегрирование этого выражения с приминением теоремы о среднем значении радиуса кривизны первого вертикала и косинуса широты для некоторой промежуточной широты называется в навигации отшествием

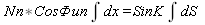
(Lam ₂ -Lam ₁)Nn*CosФиn=S*SinK=Om=ОТШ

Геометрически отшествие выражает расстояние по некоторой промежуточной параллели между меридианами пунктов прихода и отхода. Выражается в морских милях.

ПРЯМАЯ ЛОКСОДРОМИЧЕСКАЯ ЗАДАЧА

(ПЛЗ)

Это определение координат конечной точки по координатам начальной заданному начальному курсу и плаванию судна.

Изменение широты и долготы при этом на элипсоиде может быть определено:

K==Ar=Const

delФи`<sub>1</sub>=3437,8`* S/Mn *CosК

delФи=3437,8`* S/Nn *SinK/CosФи _п

Для практических расчетов вместо промежуточных широт применяется

Фи_ср=Фи₁ +delФи/2 и ПЛЗ решается по более простым формулам из локсодромического треугольника.

ПЛЗ

CosФи _п = POM/РМЧ=ОТШ/РД

(ОЛЗ)

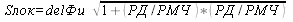
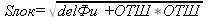
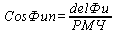
ОСНОВЫ КАРТОГРАФИИ И МОРСКИЕ КАРТЫ

Картография это наука, областю которой является постоение, издание и использование карт.

Карта это обобщенная, уменьшенное в определенном масштабе изображение поверхности земли в определенной системе координат, с указанными объектами спомощью системы условных знаков. Задача картографии — получение карты, которое сводится к изображению поверхности элипсоида на плоскости, при этом всегда будут иметь место искажения. Для оценки этих искажений вводиться понятие гауссовой кривизны:

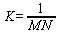Гауссова кривизна это отношение кривизны к криволинейному радиусу.

1. Плоскость: Kп = 1/R² = 1/беск.=0

2. Конус, цилиндр Кк=1/R*беск.=0

3. Сфера Кс=1/R² не равно 0 = Const

4. Элипсоид Кэл = 1/MN не равно 0 не равно Const

Из значений видно что элипсоид и сфера не могут разложиться без искажений, когда как конус и цилиндр могут.

При изображении сферы или элипсоида на конус и цилиндр можно сохранить некоторые элементы без искажений.

Вывод:

1. При изображении сферы или элипсоида на плоскости можно сохранить длины при этом искажаются площади и углы.

2. Можно сохранить углы но при этом искажаются расстояния и площади.

3. Можно сохранить площади но при этом сохраняются длины и углы

4. Можно выбрать произвольный метод изображения элементов поверхности Земли

Таким образом, исходя из решаемых задач выбирается один из способов изображения поверхности Земли на плоскости.

Все карты состоят из тивовых элементов 3х групп:

1)Оформление карты (заголовок, рамки, графики масщтабов, предупреждения и.т.д.)

2)Картографическое изображение (математическая основа и элементы содержания)

3)Дополнительные элементы (врезки, фотографии, сведения о приливах и сетки-изолинии)

Математическая основа — совокупность математических элементов карты

Математический элемент карты — это элемент, определяющий математическую связ между изображением поверхностиземного элипсоида и карты.

Основные требования к морским картам:

1. Достаточная полнота сведений, необходимых для решения поставленных задач

2. Высокая достоверность и точность изображения а так же описания

3. Простота восприятия условных знаков

4. Удобство ведения навигационной прокладки на карте и способность сохранения ее реультатов в течении длительного времени

5. Удобство ведения корректуры и малая дисформированность карты

КАРТОГРАФИЧЕСКИЕ СЕТКИ

МАСШТАБЫ

Географическая сетка координат — это сетка меридианов и параллелей на земном элипсоиде или сфере.

Картографическая сетка — это изображение сетки меридианов и параллелей на карте.

Картографическая проэкция — это отображение поверхности элипсоида или сферы на плоскости карты

Уравнение картографической поверхности — два уравнения определяющие связь между координатами точек на карте и соответствующих точек на поверхности элипсоида или сферы.

Параметры картографической проекции — постоянные величины или функции, входящие в уравнение картографической проекции.

Х=fx(Ф;Lam);

Y=fy(Ф;Lam);

P=fp(Ф;Lam);

b=fb(Ф;Lam);

xy - прямоугольные координаты

P,b - полярные координаты

Fi - параметры функции картографической проекции определяющие математический закон построения изображения на карте.

Закон, связывающий положение точки на поверхности эипсоида и на карте может быть графически или геометрически.

Отсюда следуют геометрические признаки сеток и проекции:

1. Нормальная

2. Полярная

3. Косая

4. Произвольная

На нормальной картографической сетке координатные линии изображаются в виде прямых или окружностей. Полюс проекции совмещен с географическим полюсом элипсоида или сферы.

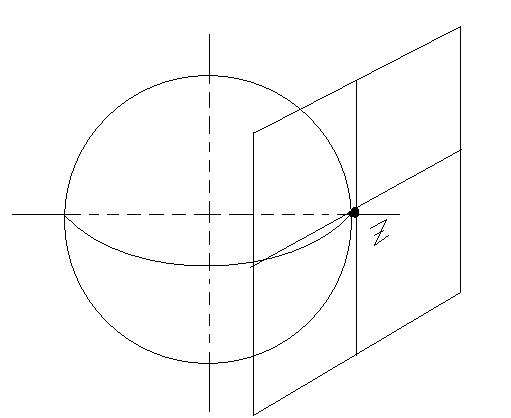
Поперечная сетка картографической проекции — на данной проекции параллели будут выглядеть параболами и гиперболами а экватор и меридианы прямыми линиями.

Косая сетка картографической проекции — сетка, полученная в случае когда применяется косая система полярных сферических координат.

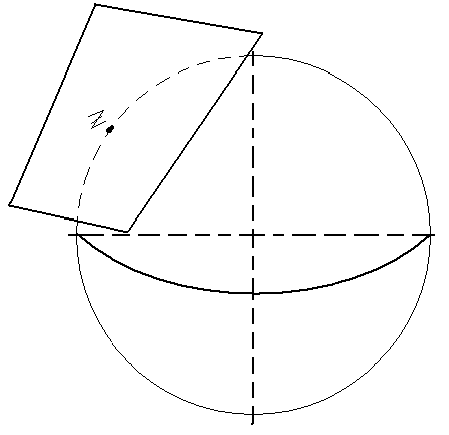
Полюс рассматриваемой системы координат раположен между экватором и географическим полюсом, меридианы и параллели на этой проекции изображаются параболами и гиперболами.

МАСШТАБ

Масштабом называется отношение длины линии на плане или карте, к соответствующей проекции этой линии на местности, иными словами масштаб это степень уменьшения горизонтального положения линии местности на карте.

Частный масштаб — отношение длины бесконечно малого отрезка на карте к дине бесконечно малого отрезка на элипсоиде.

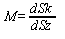
Так как элипсоид нельзя отразить без искажений на карте то частный масштаб будет наименьшим. В этой связи применяется главный масштаб. Главный масштаб это отношение, показывающее во сколько раз уменьшены линейные размеры элипсоида(сферы) при их изображении на карте.

Главный масштаб для упрощения карт назначается для главных параллелей.

Главная параллель это параллель нормальной сетки картографической проекции вдоль которой сохраняется главный масштаб.

Главный масштаб главный масштаб указывается в углу карт М₀=1/C₀

Где С₀ — знаменатель главного масштаба

Численный маштаб — масштаб дин, выраденный отличительным числом, в числителе которого всегда единица а знаменатель число, показывающее во сколько раз уменьшены линейные размеры на карте.

Например масштаб 1:5000 показывает что один сантиметр на карте соответствует 5000 сантиметрам на местности. Более крупным является тот масштаб, у которого знаменатель меньше. Например масштаб 1:1000 более крупный чем 1:25000.

Именнованный масштаб — масштаб дин, выраженный именными числами, обозначающие длины взаимно соответствующих отрезков на карте и на земном элипсоиде (1см-600м).

Линейный масштаб — графический масштаб в виде отрезков прямой разделенного на равные части с подписанными значениями соответствующих им расстояний на местности.

Поперечный масштаб — это графический масштаб в виде номограм, построение которой основанно на пропорциональности отрезков параллельных прямых, пересекающих сторону угла.

Точность масштаба - это отрезок горизонтального положения линий, соответствующий 0,1 мм на карте. Значение 0,1мм. Для определения точности масштаба принято из-за того, что это минимальный отрезок, котоапример для масштаба 1:10000 точность масштаба будет равна 1м. В этом масштабе:

1см это 10000см

1мм это 1000см

0,1мм это 100см(1м)

Увеличение масштаба это отношение частного масштаба в данной точке карты по главному направлению к главному масштабу. с=M/M₀ = C/C₀

Относительное искажение — отклонение от главного масштаба частного, выраженное в долях единиц.

Последние выражение ния показывают, что чем меньше масштаб отклоняется от единицы, тем меньше искажение изображения на карте.

Предельная точность масштаба карты это — длина линии на местности соответствующей длине на карте равная разрешающей способности глаза. Разрешающая способность глаза, принятая ИМО = 0,3мм.

M=0,3/M₀ =03*C₀

По виду меридианов и параллелей:

Круговые — меридианы и параллели показаны окружностями (используются для карт полушарий)

Коничческая — Проекция в которой углы между меридианами пропорциональны разности долгот

Азимутальная — проекция в которой параллели

Параллели — концентрические окружности проведенные из точки схождения меридианов, а меридианы являются радиальными прямыми, исходящими из одной точки (центральной), под углами равными соответствующим углам в натуре.

К частным случаям азимутальных проекций являются перспективные картографические проекции. Эти проекции применяются для составления справочных и вспомогательных карт(обзорные карты районов, ортодромические карты и ледовые)

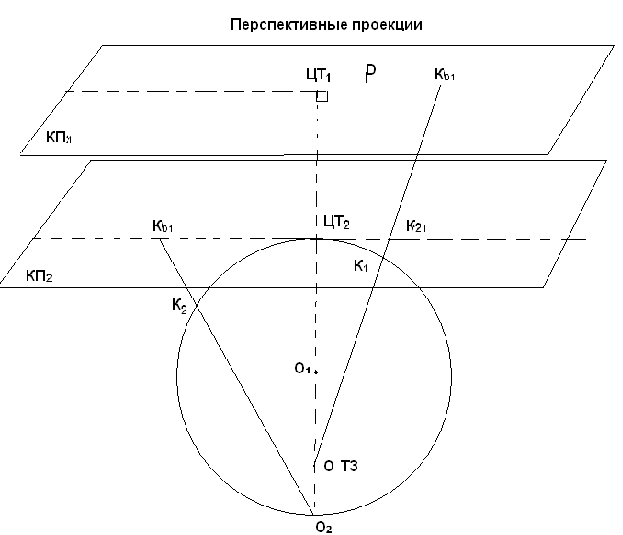
В перспективных проекциях поверхность земли (сферы) переносится на картинную плоскость методом проецирования спомощью пучка прямых, исходящих из одной точки - точки зрения (ТЗ). Картинная плоскость может отстоять от поверхности сферы на некотором расстоянии (КП₁) касаться сферы (КП₂) или пересекать её. Точка зрения (О) лежит на перпендикуляре к картинной плоскости к КП. Точку пересечения картинной плоскости с перпендикуляром называют центральной точкой карты (ЦТ). В зависимости от положения точки зрения. Одна и таже точка (К₀) будет отстоять на различных расстояниях (P) от ЦТ карты, что и будет определять характер искажений, присущих данной проекции. Наиболее распространенными перспективными проекциями является гномоническая (центральная) и стереографическая. Гномонической проекции (ТЗ в точке О₁). Сетка меридианов и параллеллей карты строится по формулам, соединяющим прямоугольные координаты точек с их географическими. В зависимости от положения центральной точки карты гномоническая проекция может быть:

1. Нормальной(полярной) — если центральная точка совмещена с географическим полюсом.

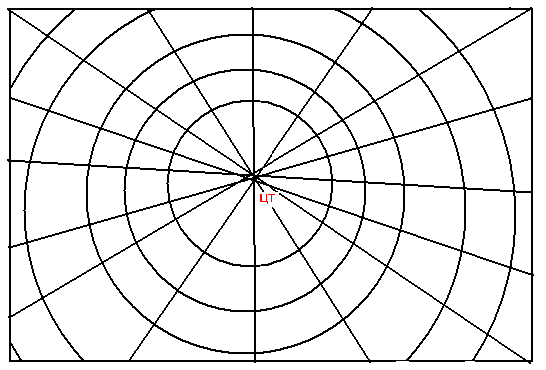
2. Экваториальная (поперечная) — Если ЦТ расположена на экваторе

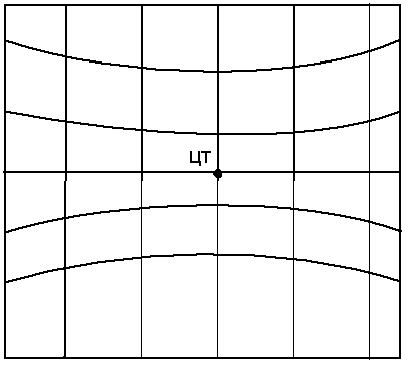
3)Косоид — ЦТ расположена в некоторой промежуточной широте.

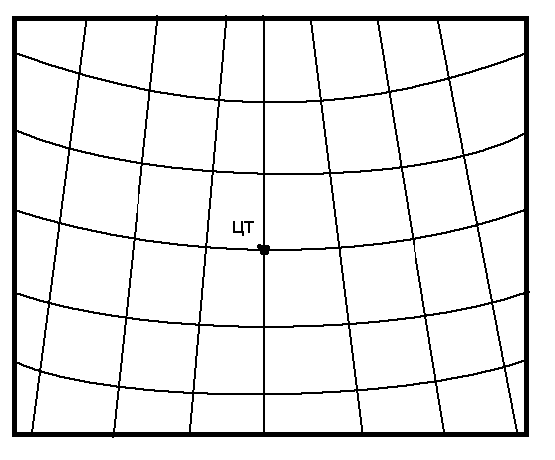
РАВНОУГОЛЬНАЯ КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ ГАУССА

Применяется для составления картографических и речных карт а так же планшетов, основной картографической сеткой этой проекции является сетка прямоугольных координат.

В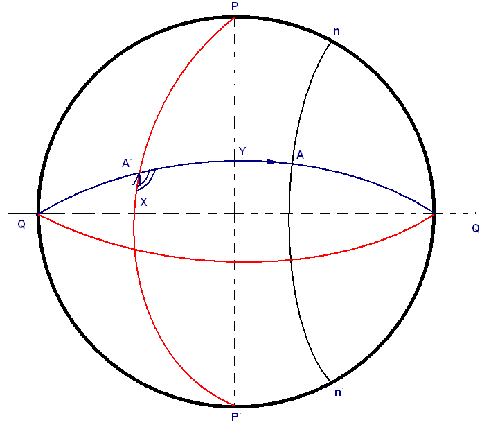 равноугольной системе координат проекции Гаусса вся поверхность земного элипсоида разбита на 60 _ 6-ти градусных зон, ограниченных меридианами. Каждая из этих зон имеет свое начало координат - точку пересечения осевого меридиана зоны с экватором.

Счет зон ведется от Гринвического меридиана к Е от N1 до N60

Любую заданную точку в пределах зоны (т.А) получают пересечением 2-х координатных линий:

1)Дуги элипса nAn на РОЛ осевому меридиану зоны

2)Кратчайшей линии AA` проведенной из точки А перпендикулярно осевому меридиану.

За начало в каждой зоне принимается пересечение осевого меридиана с экватором.

Определяется абциссой X а удаление малого круга nn` от осевого меридиана ординатой Y.

Абциссы X во всех зонах отсчитываются в обе стороны от экватора (“+”- к N;) Ординате Y приписывается знак «+» если заданная точка удалена к E и знак «-» к W.

Для определения отечественного номера зоны, в которой расположена заданная точка с долготой (λ) применяют формулу:

n=(λ+3°)/6 деление долготы λ производится до ближайшего целого числа. Для вычисления долготы осевого меридиана зоны (L₀)применяют формулу:

L₀ = 6*n-3°

Для n=10; L₀ = 57°E

При заданной долготе

λ=58°W и λ=360°-58°=308°E а значит n=51, L₀=303° или 57°

N – международная нумерация зон от меридиана 180 к востоку

Для λ_E : N=n+30 и n=N-30 (для восточного полушария)

Для λ_W : N=n+30 и n=N+30 (для западного полушария)

В таблицах МТ-2000 т2.31а приведены отечественные значения.

Граничными линиями карт в проеккции Гаусса служат меридианы и параллели, положение заданной точки на карте получают указанием плоских прямоугольных координат X и Y этим координатам соответствуют киллометровые линии:

X=Const парралельно экватору

Y=Const параллельно осевому меридиану

Плоские координаты XY являются функциями географических координат точки.

l = λ- L₀

Фид функций f₁ и f₂ выводится так, чтобы обеспечивалось свойство равноугольности проекции при постоянном масштабе вдоль осевого меридиана зон. Киллометровые линии это линии одинаковых значений абцисс X=Const или ординат Y=Const, выраженные целым числом км. Километровые линии это 2 семейства взаимноперпендикулярных прямых и оцифровываются соответствующими зачениями координат в киллометрах. На картах проекции Меркатора линии X изображаются кривыми, обращенными выпуклостями к полюсу, а линии Y кривыми, выпуклостью к осевому меридиану и расходящимся по мере удаления от экватора.

Рамки карт в проекции Гаусса разбиты на минуты по широте и долготе, значением широт и долгот параллелей и меридианов, ограничивающих карту надписываются в углах рамки. Меридианы и параллели на карту не наносятся.

Угол между киллометровой линией Y=Const и истинным меридианом называется схождением меридиана этот угол отсчитывается от северной части истинного меридиана по часовой стрелке до северной части киллометровой линии Y=Const. Схождению меридианов(GAM) приписывают знак «+» если заданная точка расположена к E (восстоку) от осевого меридиана и «-» если к западу от осевого меридиана. При известных меридианах φ λ угол схождения меридианов вычисляется по формуле:

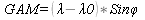
Нормальная равноугольная цилиндрическая проекция (проекция Меркатора)

Приобрела всеобщее распространение для составления морских карт, названа в честь голандского ученого, который её предложил. Посторение этой проекции производится проектированием глобуса из его центра на боковую поверхность цилиндра касательного к экватору. После проектирования цилиндр разрезается по образуещей и и разворачивается на плоскость. При проектировании на поверхность цилиндра параллели растягиваются до длины экватора соответственно на такуюже величину растягиваются и меридианы. Поэтому проекция сохраняет подобие фигур и является равноугольной

Карты в Меркарторской проекции имеют следующие свойства:

1)Меридианы и параллели изображаются взаимно перпендикулярными линиями.

2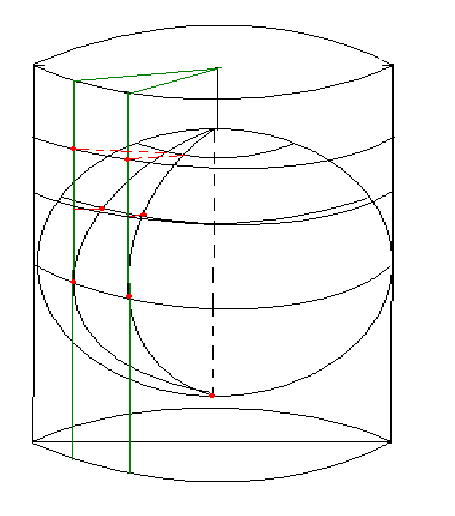)Расстояния между меридианами одинаковые а между параллелими увеличиваются с увеличением широты

3)Сохраняется равенство углов и подобие фигур

4)Масштаб переменный и с увеличением широты становится крупенее

5)Поэтому расстояние между 2мя точками определяется по специальной шкале нанесенной на боковых обрезках карты. Эта шкала учитывет переменный масштаб по широте. 5) Искажение маштаба практически неощутимо только в полосе 5 градусов от экватора.

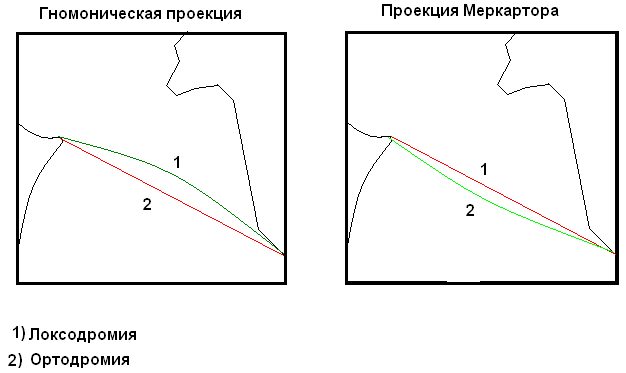
Локсодромия изображается прямой линией что является преимуществом проекции. Ортодромияизображается кривой линией, выпуклой к полюсу.

ПОСТРОЕНИЕ МЕРКАРТОРСКОЙ КАРТЫ

Должны быть известны:

Широта северной рамки карты

Широта южной рамки карты

Долгота восточной

Долгота западной

Интервалы нанесения параллелей и меридианов.

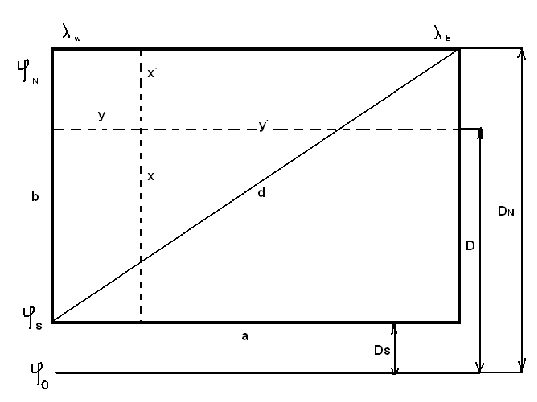
Для проверки графических построении вычисляется диагональ рамки карты:

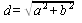
Для контроля расчитывают от северной и южной рамок карты положение параллелей:

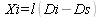
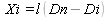
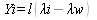
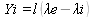
С той же целью определяют от восточной и западной рамок карты меридиан:

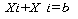
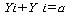
ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ПРОЕКЦИИ

При построении карт используются разные проекции как по характеру искажений так и по способу остроений.

При плавании во всех районах нашла применение проекция меркартора

Перспективные проекции применяются для составления некоторых справочных и вспомогательных карт и представляют собой частный случай азимутальных проекциций

Равноугольная проекция Гаусса применяестя для составления топографических и речных карт. Основой этой проекции является сетка прямоугольных координат.

ТЕОРИЯ ОПРЕДЕЛЕНИЯ И ОЦЕНКА ТОЧНОСТИ КООРДИНАТ МЕСТА СУДНА

Навигационные параметры и изолинии

Обсервация (определение места судна)- процесс измерения и обработки навигационных параметров, результатом которого является обсервованное место судна(в виде координат или точки на карте).

Обсервованное место судна — место, координаты которого получены пересечением двух или более обсервованных изолиний (линий положения).

Навигационные параметры (НП) — измеряемые судовыми техническими средствами физические величины, определяющие положение судна в море.

Радионавигационный параметр(РНП) — параметр или отношение параметров радионавигационного поля, используемый для определения НП и сязанную с ним функциональную зависимость.

В каждой точке на поверхности земли. НП связан определенными функциями с координатами.

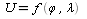
Если на поверхности земли, представленной на карте нанести различные значения навигационных параметров то получим значения определяемые вышеуказанными формулами. Среди параметров можно найти с одинаковыми значениями.

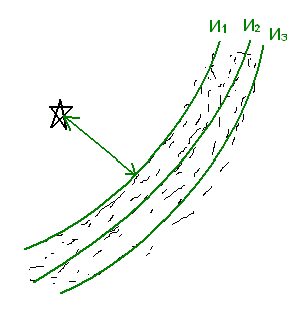
Изолиния или навигационная изолиния — геометрическое место точек на земной поверхности, принятой за элипсоид или сферу, которая однозначно соответствует постоянному значению НП.

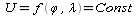
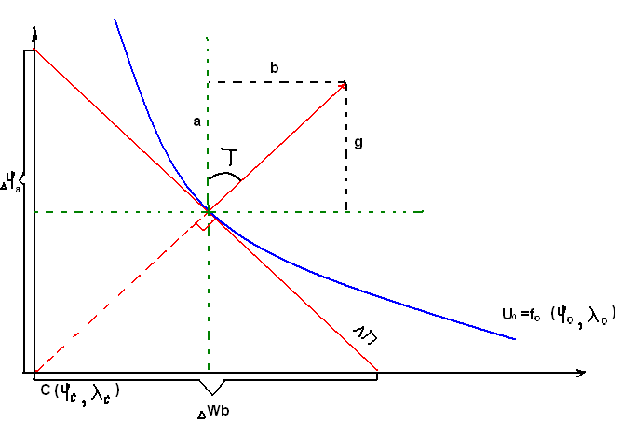
ГРАДИЕНТ ИЗОЛИНИИ

Для характеристики НП применяется величина, характеризующяя скорость его изменения — ГРАДИЕНТ.

Градиент навигационной изолинии — это пространственный вектор, касательный к поверхности земли, перпендикулярный к изолинии, направленный всторону возрастания НП и характеризующий скорость его изменения.

Градиент всегда имеет размерность.

В любой точке на изолинии можно получить составляющий градиента по меридиану и параллели.

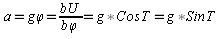
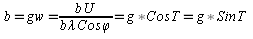
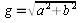
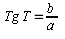
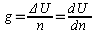
- приращение НП

n – смещение (перенос) изолинии

T – направление градиента

ОБОБЩЕННЫЙ МЕТОД ЛИНИЙ ПОЛОЖЕНИЯ

Опредеделение обсервованных координат места судна сводится к аналитическому или графическому решению двух уравнений и определению точки их пересечения.

Уравнение изолиний как правило транцидентные и их решение связанос с большими сложными вычислениями.

Для простых изолиний (геометрических) их решение может быть осуществлено геометрически на карте. Учитывая, что изолинии кривые то их совместное решение дает многозначность. От недостатков методов изолиний позволяет избавится обобщенный метод линий положения, разработанный Коврайским В.В., в 1909г. Суть этого метода сводится к следующему:

1. В любой момент известны координаты судна

2)

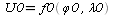
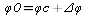
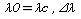
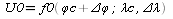
3)Вычисляем счислымий НП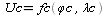

4)Учитывая малую кривизну изолинии ее отрезок вблизи счислимого места заменяется прямой, касательной к изолинии.

Линия положения(ЛП) — касательная к изолинии определяющая точке ближайший к счислимому месту(на перппендикуляре к изолинии из счислимого места — градиенте).

На языке математики замена кривой линии прямой называется линией оризации. И сводится к разложении функции кривой в ряд Тейлора.

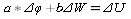- Уравнение ЛП в общем виде

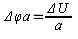
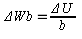- построение ЛП через точки пересечения

По выше указанным уравнениям невозможно построить ЛП параллельную меридианам или параллелям, одна из точек пересечения за пределами карты, проекции градиентов близки или равны нулю. От этого едостатка можно освободиться переходом от общего уравнение ЛП к уравнению в нормальном виде.

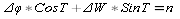- уравнение нормального вида

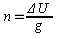- Перенос ЛП

Спомощью Т и n а также навигационных инструментов можно проложить ЛП относительно счислимого места судна без всяких ограничений.

Задача определения места судна сводится к решению системы 2х линейных уравнений ЛП. При замене изолиний линиями положения в обсервованное место вводится методическая погрешность. Как правило она очень мала и ей можно пренебречь. При необходимости исключения методических погрешностей пользуются методом итерраций. Как правило для навигационных измерений достаточно одной итеррации.

ОПРЕДЕЛЕНИЕ КООРДИНАТ МЕСТА СУДНА ОБОБЩЕННЫМ МЕТОДОМ ЛП

(АНАЛИТИЧЕСКОЕ РЕШЕНИЕ)